Class 11 Maths Chapter 2 Relations And Functions Exercise 2.3 Solutions in English Medium

Class 11 Maths Chapter 2 Relations And Functions Exercise 2.3 Solutions in English Medium

 

Free NCERT Solutions for Class 11 Maths Chapter 2 Relations And Functions Exercise 2.3 prepared by expert Mathematics teacher as per CBSE (NCERT) books guidelines.

 

Free  NCERT Solutions for Class 11 Math’s Chapter 2  Relations And Functions Exercise 2.1, Exercise 2.2, Exercise 2.3 and Miscellaneous Exercise in English Medium for CBSE.

 

NCERT Maths Class 11 Chapter 2 Relations And Functions. Just click on the Exercise wise links given below to practice the Maths solutions for the respective exercise.

Exercise 2.1	Click here
Exercise 2.2	Click here
Exercise 2.3	Click here

Class 11 Maths Chapter 2 Relations And Functions Exercise 2.3 Solutions in English Medium

 

Exercise 2.3 Class 11 Maths Question no 1

Exercise : 2.3

 

1.  Which of the following are functions? Give reasons. If it is a function determine its domain and range.

(i) {(2, 1), (5, 1), (8, 1), (11, 1), (14, 1), (17, 1)}

(ii) {(2, 1), (4, 2), (6, 3), (8, 4), (10, 5), (12, 6), (14, 7)}

(iii) {(1, 3), (1, 5), (2, 5)}

Solution-

(i) We have the given relation as, {(2,1),(5,1),(8,1),(11,1),(14,1),(17,1)}.

Thus, we can see, the domain of the relation consists of {2,5,8,11,14,17}

 and range is {1}.

And we also have, every element of the domain is having their unique images, then it is a function.

 

 (ii)  {(2,1),(4,2),(6,3),(8,4),(10,5),(12,6),(14,7)}

Solution:-

 We have our given relation, {(2,1),(4,2),(6,3),(8,4),(10,5),(12,6),(14,7)}

Thus, we have our domain as, {2,4,6,8,10,12,14}

 and range as, {1,2,3,4,5,6,7}

Every element of the domain is having their unique images, so this is a function.

 

(iii) {(1,3),(1,5),(2,5)}

Solution:-

Our given relation is, {(1,3),(1,5),(2,5)}

From the domain of the relation the element 1

 is having two different images 3,5

So, every element of the domain is not having their unique images. So, this is not a function.

 

Exercise 2.3 Class 11 Maths Question no 2

2. Find the domain and range of the following real functions:

(i) f(x) = -|x|                                      (ii) f(x) =  √(9 - x²)

Solution :-

 

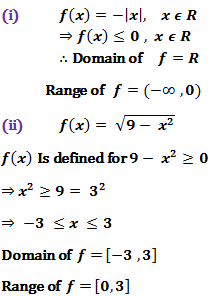
Exercise 2.3 Class 11 Maths Question no 3

3. A function f  is defined by f(x) = 2x –5. Write down the values of

(i) f (0),   (ii) f (7), (iii) f (–3).

Solution :-

Given:  f(x) 2x - 5

(i)  Putting We have the given function as, f(x)=2x−5

So, the value of,

f(0)=2×0−5=−5

 

(i)  We have the given function as, f(x)=2x−5

 So, the value of,

f(7)=2×7−5=14−5=9

 

(ii)  We have the given function as, f(x)=2x−5

 So, the value of,

f(−3)=2×(−3)−5

            =−6−5

            =−11

 

Exercise 2.3 Class 11 Maths Question no 4

4. The function t which maps temperature in degree Celsius into temperature in degree Fahrenheit is defined by  

(i) t(0)     (ii) t(28)    (iii) t(-10)  (iv) The values of C, When t(C) = 212

Solution:-

Exercise 2.3 Class 11 Maths Question no 5

 

5. Find the range of each of the following functions.

(i) f (x) = 2 – 3x, x ∈  R , x > 0.

(ii) f (x) = x 2 + 2, x is a real number.

(iii) f (x) = x, x is a real number.

Solution :

 

(i) f(x) = 2 – 3x, x ∈ R, x > 0

The values of f(x) for various values of real numbers x > 0 can be written in the tabular form as

X         0.01           0.1         0.9        1        2        2.5             4          5         . . . . .  .

F(X)  1.97          1.7          -0.7        -1      -4        -5.5         -10       -13     . . . . . .

 

Thus, it can be clearly observed that the range of f is the set of all real numbers less than 2.

i.e., range of  f = (–∞, 2)

Alter:

Let x > 0

⇒ 3x > 0

⇒ 2 –3x < 2

⇒ f(x) < 2

∴Range of f = (–∞, 2)

 

(ii) f(x) = x² + 2, x, is a real number

The values of f(x) for various values of real numbers x can be written in the tabular form as

X            0     ±0.3     ±0.8         ±1         ±2         ±3    . . . . . . . . .

f(X)      2    2.09       2.64            3            6            11    . . . . . . . . .

 

Thus, it can be clearly observed that the range of f is the set of all real numbers greater than 2.

i.e., range of f = [2, ∞)

Alter:

Let x be any real number.

 

Accordingly,

X² ≥ 0

⇒ x² + 2 ≥ 0 + 2

⇒ x² + 2 ≥ 2

⇒ f(x) ≥ 2

∴ Range of f = [2,∞)

 

(iii) f(x) = x, x is a real number

It is clear that the range of f is the set of all real numbers.

∴ Range of f = R 

 

Published  By Lokesh Das

NCERT textbook Solutions for class 9  in Assanese medium.  

More Resours For Class 10 Solutions in Assamese Medium

• Class 10 Maths Solutions
• Class 10 Science Solutins
• Class 10 Social Science Solutions
• Class 10 Assamese Solutions
• Class 10 English Solutions
• Class 10 Hindi Solutions
• Class 10 Advanced Geography Solutions 

 NCERT textbook Solutions for class 10  in Assanese medium.  

     More Resourses For Class 9 Solutions in Assamese Medium

• Class 9 Maths Solutions
• Class 9 Science Solutins
• Class 9 Social Science Solutions
• Class9 Assamese Solutions
• Class9 English Solutions
• Class 9 Hindi Solutions
• Class 9 Advanced Geography Solutions

More Resours For Class 10 Solutions in Assamese Medium

• Class 10 Maths Solutions
• Class 10 Science Solutins
• Class 10 Social Science Solutions
• Class 10 Assamese Solutions
• Class 10 English Solutions
• Class 10 Hindi Solutions
• Class 10 Advanced Geography Solutions 

CLASS 11 English MEDIUM NCERT SOLUTIONS. CLASS 11 MATHEMATICS SOLUTIONS IN ENGLISH MEDIUM. CLASS 11 MATHEMATICS RELATIONS AND FUNCTIONS CHAPTER SOLUTIONS IN ENGLISH MEDIUM. CLASS 11 MATHS  RELATIONS AND FUNCTIONS EXERCISE 2.3 SOLUTIONS IN ENGLISH MEDIUM.